Contact Information
Dr Paolo Tiso
Senior Scientist
Institute for Mechanical Systems
LEE M 205
Leonhardstrasse 21
8092 Zürich, Switzerland
Tel.: +41 44 632 36 41
Email: ptiso{at}ethz.ch
Substructuring for geometrically nonlinear structural dynamics
Reduction of the computational burden for the reduced nonlinear terms
Model order reduction via nonlinear manifolds
Efficient modeling techniques for kites for power generation
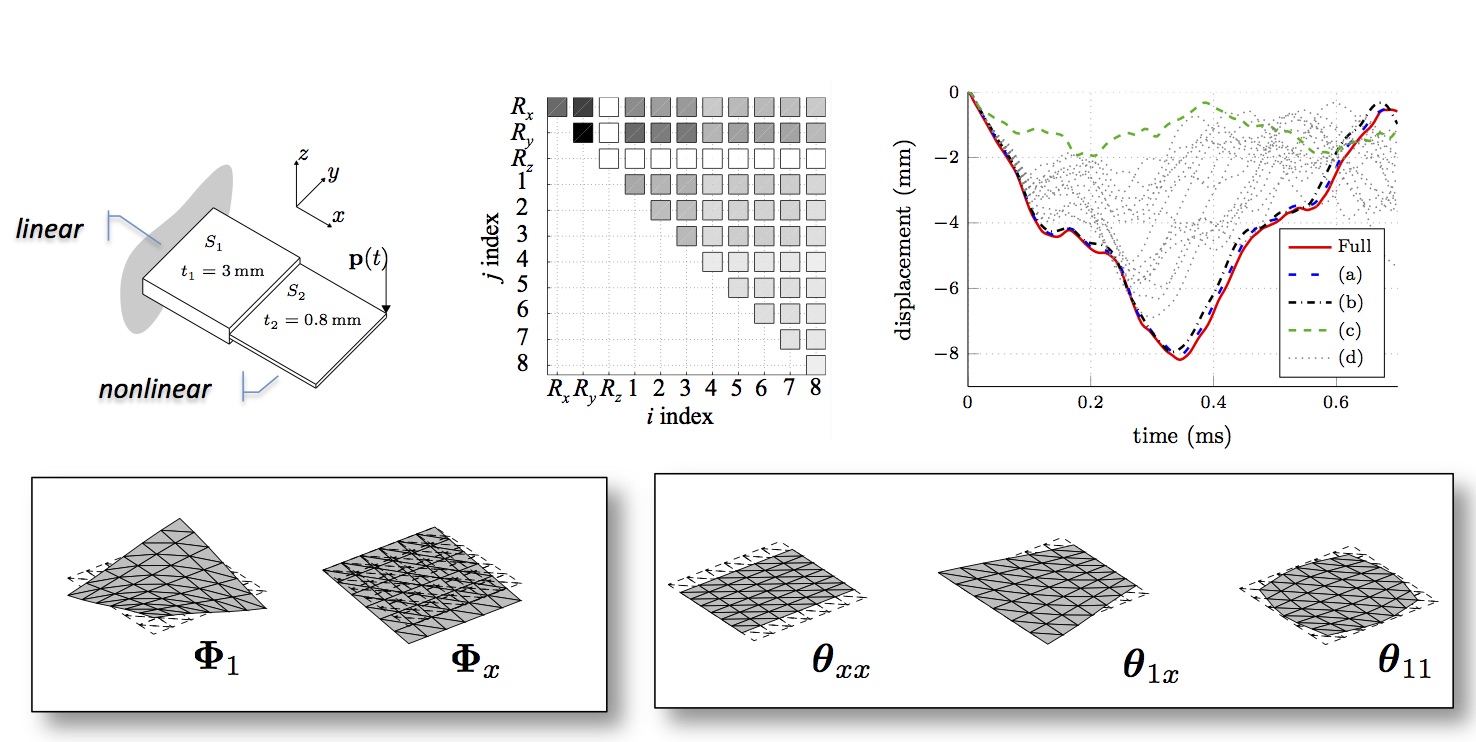
Widely used substructuring techniques such as Craig-Bampton and Rubin-McNeal are extended to deal with components nonlinearities in a reduced setting. The nonlinearities can be either concentrated or distributed (i.e. geometrically nonlinear components). The nonlinearity can be confined only to the corresponding components of the system and therefore reduce the overall computational cost.
Collaborators: F. Wenneker and L. Wu
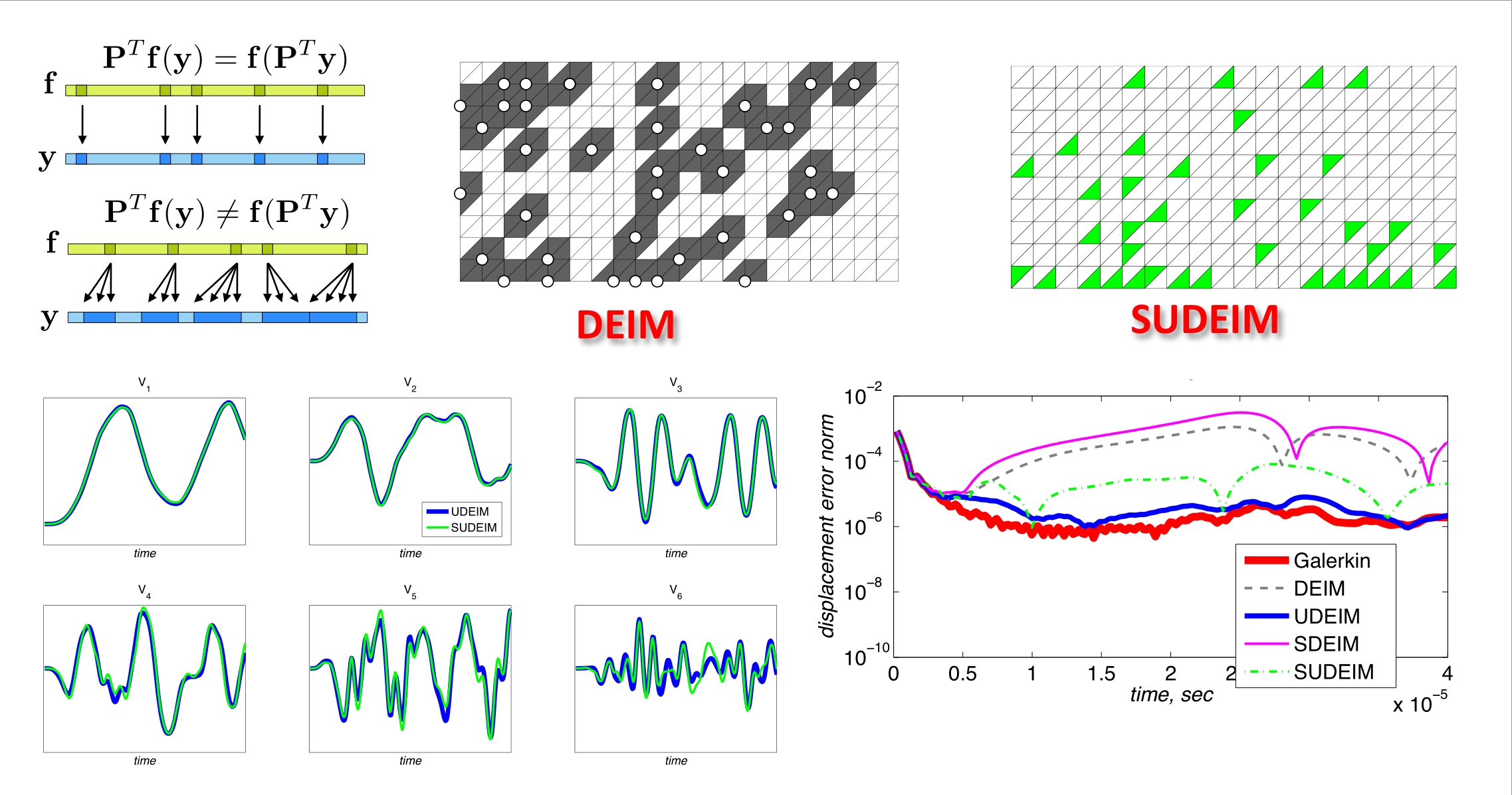
The project goal is an effective approximation of the nonlinear internal restoring forces in dynamic problems via the Discrete Empirical Interpolation Method (DEIM). DEIM must be adapted to handle the Finite Element Method effectively. The outcome of this research will allow to drastically reduce the computational time of the nonlinear terms when coupled with a Galerkin reduction method. The DEIM method has been successfully modified and improved to effectively tackle Finite Element discretized problems. More recently, a computationally affordable implementation of the Energy Conserving Sampling and Weighting (ECSW) method has been investigated for geometrically nonlinear structural dynamics problems.
Collaborators: S. Jain, R. Dedden and D. Rixen
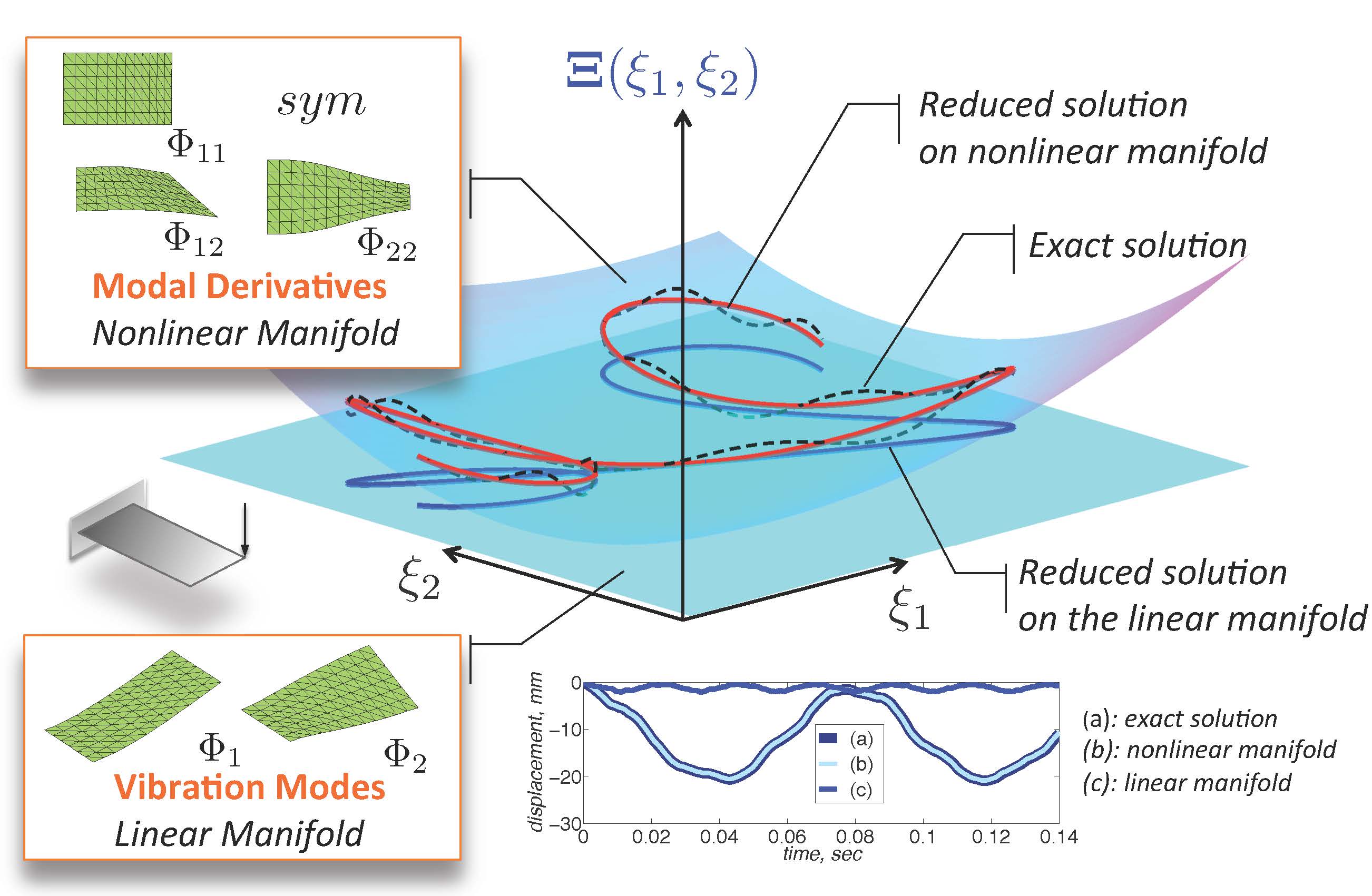
We investigate the possibility of reducing a large size model by resorting on a nonlinear mapping between few generalized coordinates and the primal unknowns. This approach can minimize the size of the reduced order model by exploiting the physics of the solution. The focus is on an affordable and reliable construction of such manifolds. Two different methods have been investigated: modal derivatives and nonlinear force condensation. The former has been successfully applied in a flexbile multibody context.
Collaborators: L. Wu, J. Rutzmoser, D. Rixen and G. Haller
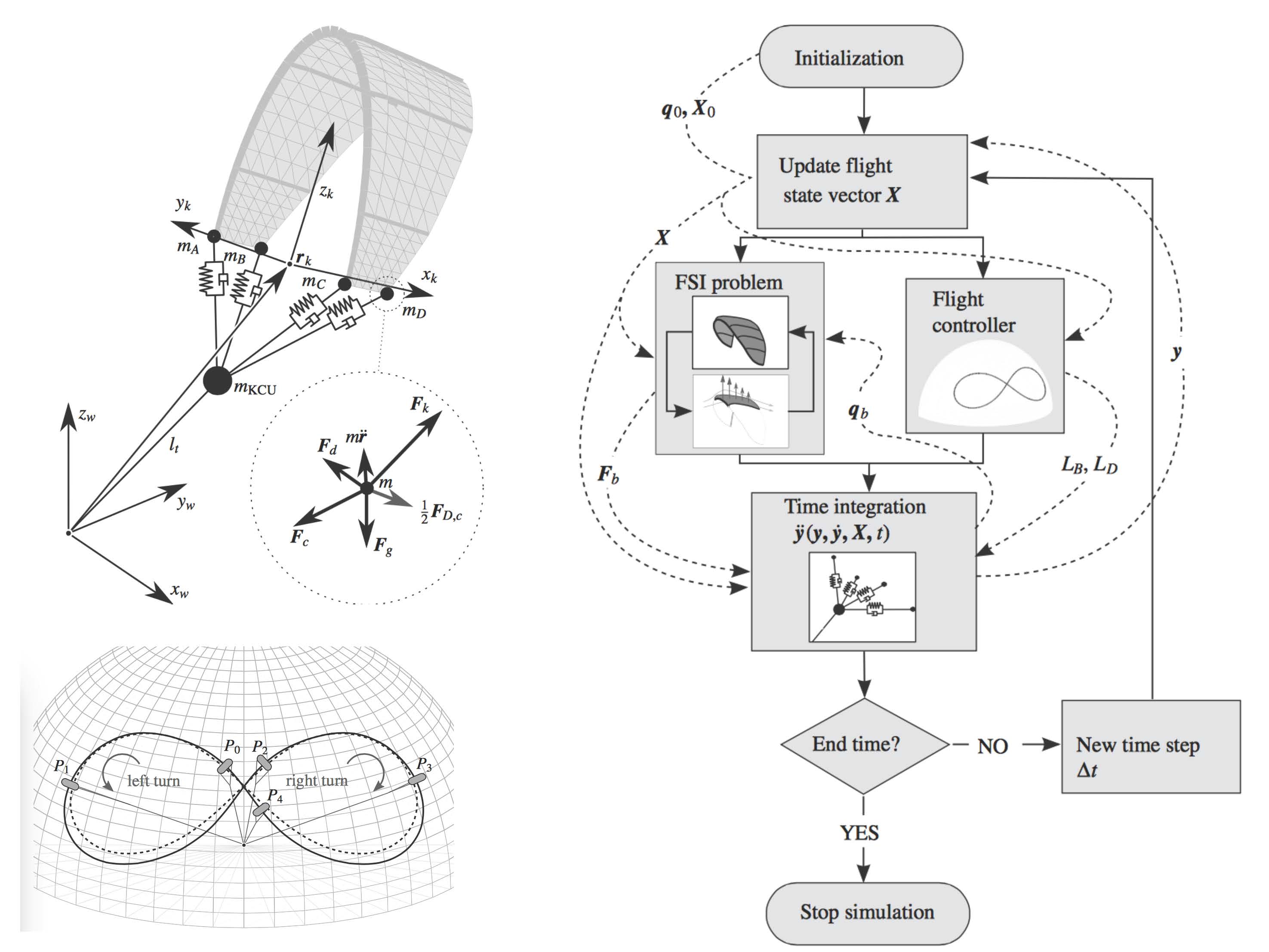
The project goal is the development of efficient, quasi real time realistic models of kites for electric power
generation. The model must contain nonlinear geometrical effects to account for the large deformations,
(un)steady aerodynamics, aeroelastic coupling, system dynamics and control law for the tracking of optimal
trajectory. The research heavily relies on state of the art model order reduction techniques and
multifield modeling.
Collaborators: A. Bosch, R. Schmehl and D. Rixen